The LCR parallel resonance circuit stands as a pivotal component in the realm of electronics, providing a cornerstone for many applications across various fields. This circuit, characterized by its combination of inductors (L), capacitors (C), and resistors (R), is renowned for its ability to resonate at a particular frequency known as the resonant frequency. Understanding the nuances of this circuit is crucial for anyone delving into advanced electronics or physics, as it forms the basis of numerous innovations and technologies we rely on today.
Through this comprehensive guide, we aim to dissect the intricacies of the LCR parallel resonance circuit, elucidating its principles, functionalities, and practical applications. For students, educators, and professionals alike, our exploration into this subject matter will offer valuable insights into the mechanisms that govern resonance and how it can be harnessed effectively. With its optimal design and configuration, the LCR parallel resonance circuit provides a robust framework for achieving high levels of efficiency and performance in electronic systems.
Electronics enthusiasts often encounter the LCR parallel resonance circuit when pursuing projects involving signal processing, telecommunications, or radio frequency applications. It's essential to grasp the fundamental concepts to optimize circuit design and troubleshoot potential issues. Whether you're a novice in the field or an experienced engineer, this article aims to equip you with the knowledge and tools necessary to master the LCR parallel resonance circuit and leverage its capabilities in your ventures.
Table of Contents
- Principles of Resonance
- Components of LCR Circuit
- How Does an LCR Parallel Resonance Circuit Work?
- Importance of Resonant Frequency
- Calculating Resonant Frequency
- Applications of LCR Parallel Resonance Circuit
- What Are the Benefits of Using an LCR Parallel Resonance Circuit?
- Limitations and Challenges
- LCR Parallel Resonance Circuit in Radio Frequency
- Impedance and Bandwidth
- How Can You Optimize an LCR Parallel Resonance Circuit?
- Troubleshooting Common Issues
- Future Developments in LCR Parallel Resonance Circuits
- Frequently Asked Questions
- Conclusion
Principles of Resonance
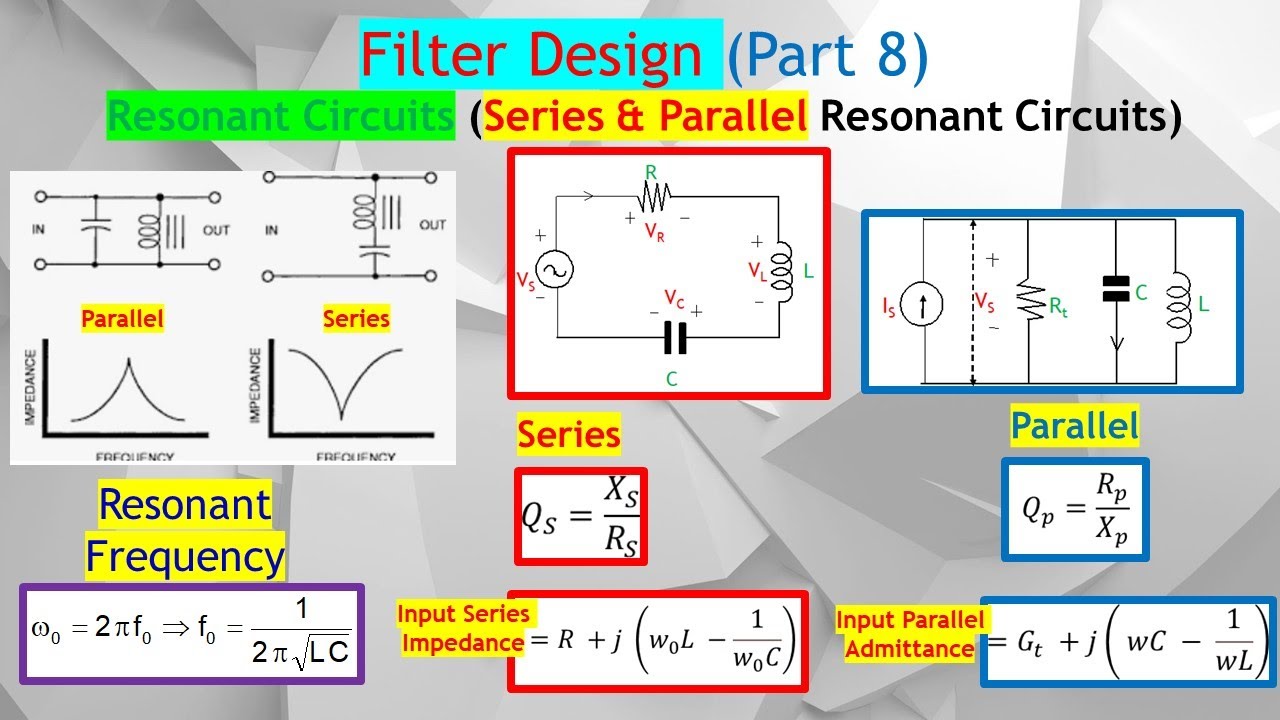
Resonance is a phenomenon that occurs when a system oscillates at its maximum amplitude due to an external force or a periodic input. The concept is central to understanding the LCR parallel resonance circuit, as it directly impacts how the circuit behaves under certain conditions. In the context of an LCR circuit, resonance is achieved when the inductive reactance and capacitive reactance are equal in magnitude but opposite in phase. This balance allows for the maximum transfer of energy between the inductor and capacitor, resulting in minimal energy loss.
At resonance, the circuit exhibits unique characteristics, such as a peak in voltage across the inductor or capacitor, while the impedance reaches its minimum. This condition allows the circuit to effectively filter specific frequencies, making it an essential component in applications like radio receivers and transmitters. Understanding the principles of resonance is vital for designing circuits that can efficiently process or transmit signals.
The resonance frequency depends on the values of the inductor and capacitor, which can be adjusted to achieve the desired frequency response. The mathematical relationship governing this frequency is derived from the formula: \( f_r = \frac{1}{2\pi\sqrt{LC}} \). Here, \( f_r \) represents the resonant frequency, \( L \) is the inductance, and \( C \) is the capacitance. By manipulating these values, engineers can tailor the circuit's response to suit various applications.
Components of LCR Circuit
The LCR parallel resonance circuit is composed of three primary components: the inductor (L), the capacitor (C), and the resistor (R). Each component plays a crucial role in determining the circuit's overall behavior and performance.
The Inductor (L)
Inductors are passive components that store energy in the form of a magnetic field when an electric current flows through them. In the LCR parallel circuit, the inductor's role is to oppose changes in current, thereby stabilizing the circuit during resonance. The inductance value, measured in henrys (H), influences the resonant frequency and is a critical parameter in circuit design.
The Capacitor (C)
Capacitors are devices that store electrical energy in an electric field, enabling them to release and absorb energy as required. In the LCR circuit, capacitors work in tandem with inductors to achieve resonance. The capacitance value, measured in farads (F), directly affects the resonant frequency and the circuit's ability to filter specific frequencies.
The Resistor (R)
Resistors are components that limit the flow of electrical current in a circuit, dissipating energy as heat. In the LCR parallel circuit, the resistor plays a crucial role in determining the circuit's quality factor (Q factor), which is a measure of how selective the circuit is in filtering frequencies. A higher Q factor indicates a narrower bandwidth and greater selectivity.
By carefully selecting and configuring these components, engineers can design LCR parallel resonance circuits that meet specific requirements, ensuring optimal performance and efficiency in various applications.
How Does an LCR Parallel Resonance Circuit Work?
The LCR parallel resonance circuit operates on the principle of resonance, where the inductive and capacitive reactances are equal and opposite. At this point, the circuit's impedance is minimized, allowing for maximum energy transfer between the inductor and capacitor. This condition enables the circuit to effectively filter and process specific frequencies, making it an essential component in various electronic applications.
When an alternating current (AC) source is connected to the LCR parallel circuit, the current flows through the inductor, capacitor, and resistor. The inductor and capacitor store and exchange energy, while the resistor dissipates energy as heat. At the resonant frequency, the energy exchange between the inductor and capacitor is maximized, resulting in minimal energy loss and a peak in voltage across the components.
The circuit's behavior can be analyzed using complex impedance and phasor diagrams, which help visualize the relationship between voltage, current, and impedance at different frequencies. By understanding these relationships, engineers can design circuits tailored to specific applications, optimizing performance and efficiency.
Importance of Resonant Frequency
The resonant frequency is a critical parameter in the design and operation of an LCR parallel resonance circuit. It determines the circuit's ability to filter specific frequencies and affects its overall performance and efficiency. By carefully selecting the values of the inductor and capacitor, engineers can achieve the desired resonant frequency, ensuring optimal circuit behavior for a given application.
Resonant frequency plays a crucial role in various applications, such as:
- Signal Processing: In communication systems, resonant frequency is essential for filtering and processing signals, ensuring clear and accurate transmission and reception.
- Radio Frequency Applications: Resonant circuits are used in radio transmitters and receivers to isolate and amplify specific frequencies, enabling efficient communication over long distances.
- Power Systems: Resonant frequency is used in power systems to minimize energy loss and improve efficiency, ensuring optimal performance and reliability.
Understanding the importance of resonant frequency is crucial for designing and optimizing LCR parallel resonance circuits, ensuring their effective application in various fields.
Calculating Resonant Frequency
Calculating the resonant frequency of an LCR parallel resonance circuit is essential for optimizing its design and performance. The resonant frequency depends on the values of the inductor and capacitor, and can be determined using the formula:
\( f_r = \frac{1}{2\pi\sqrt{LC}} \)
Where:
- \( f_r \) is the resonant frequency (in hertz)
- \( L \) is the inductance (in henrys)
- \( C \) is the capacitance (in farads)
By manipulating the values of the inductor and capacitor, engineers can achieve the desired resonant frequency, ensuring that the circuit effectively filters and processes specific frequencies. This process involves selecting appropriate component values and configuring the circuit to meet specific requirements.
Calculating the resonant frequency is a crucial step in the design and optimization of LCR parallel resonance circuits, enabling engineers to tailor the circuit's response to suit various applications.
Applications of LCR Parallel Resonance Circuit
The LCR parallel resonance circuit is a versatile component used in a wide range of applications across various fields. Its ability to filter and process specific frequencies makes it an essential tool for engineers and designers working in electronics, telecommunications, and signal processing.
Some common applications of LCR parallel resonance circuits include:
- Radio Transmitters and Receivers: LCR circuits are used to isolate and amplify specific frequencies, enabling efficient communication over long distances.
- Signal Processing: In communication systems, resonant circuits are used to filter and process signals, ensuring clear and accurate transmission and reception.
- Power Systems: Resonant circuits are used to minimize energy loss and improve efficiency, ensuring optimal performance and reliability.
- Oscillators: LCR circuits are used in oscillators to generate stable and precise frequencies for various applications, such as timing and frequency synthesis.
- Filters: Resonant circuits are used in filters to selectively pass or block specific frequencies, enabling precise control over signal processing.
The versatility and functionality of LCR parallel resonance circuits make them indispensable components in various applications, providing engineers with the tools necessary to design and optimize electronic systems for a wide range of purposes.
What Are the Benefits of Using an LCR Parallel Resonance Circuit?
The use of an LCR parallel resonance circuit offers several benefits, making it a valuable component in the design and optimization of electronic systems. Some of the key advantages include:
- Efficient Energy Transfer: At resonance, the circuit achieves maximum energy transfer between the inductor and capacitor, resulting in minimal energy loss and improved efficiency.
- Selective Frequency Filtering: The circuit's ability to filter specific frequencies makes it an essential tool for applications such as signal processing and telecommunications.
- Versatility: The LCR parallel resonance circuit can be used in a wide range of applications, from radio transmitters and receivers to power systems and oscillators.
- Cost-Effective: The use of readily available components, such as inductors, capacitors, and resistors, makes the circuit a cost-effective solution for various applications.
- Customization: By adjusting the values of the inductor and capacitor, engineers can tailor the circuit's response to meet specific requirements, ensuring optimal performance and efficiency.
The benefits of using an LCR parallel resonance circuit make it an indispensable tool for engineers and designers working in electronics, providing them with the tools necessary to achieve optimal performance and efficiency in their projects.
Limitations and Challenges
While the LCR parallel resonance circuit offers numerous benefits, it also presents certain limitations and challenges that engineers must consider when designing and optimizing electronic systems. Some of these challenges include:
- Component Variability: The performance of the circuit is highly dependent on the values of the inductor, capacitor, and resistor, which can vary due to manufacturing tolerances and environmental factors.
- Limited Bandwidth: The circuit's selectivity results in a narrow bandwidth, which may limit its applicability in certain applications that require a broader frequency response.
- Sensitivity to Temperature: Changes in temperature can affect the performance of the circuit, leading to variations in the resonant frequency and impedance.
- Complexity of Design: Designing an LCR parallel resonance circuit requires a thorough understanding of the principles of resonance, impedance, and frequency response, making it a challenging task for novice engineers.
Despite these challenges, the LCR parallel resonance circuit remains a valuable tool for engineers and designers, providing them with the means to achieve optimal performance and efficiency in various applications. By understanding and addressing these limitations, engineers can design circuits that effectively meet the demands of their projects.
LCR Parallel Resonance Circuit in Radio Frequency
The LCR parallel resonance circuit plays a crucial role in radio frequency (RF) applications, where it is used to isolate and amplify specific frequencies, enabling efficient communication over long distances. The circuit's ability to filter and process RF signals makes it an essential component in radio transmitters and receivers, ensuring clear and accurate transmission and reception.
In RF applications, the LCR circuit is used to tune the frequency response of the system, allowing it to selectively pass or block specific frequencies. This process involves adjusting the values of the inductor and capacitor to achieve the desired resonant frequency, ensuring optimal signal processing and communication.
The use of LCR parallel resonance circuits in RF applications provides several benefits, including improved signal clarity, reduced interference, and enhanced communication range. By understanding the principles of resonance and frequency response, engineers can design and optimize RF systems that effectively meet the demands of their applications.
Impedance and Bandwidth
The concepts of impedance and bandwidth are central to understanding the behavior of an LCR parallel resonance circuit. These parameters directly affect the circuit's performance and efficiency, making them critical considerations in the design and optimization process.
Impedance
Impedance is a measure of the opposition to the flow of alternating current in a circuit. In an LCR parallel resonance circuit, impedance is a complex quantity that depends on the values of the inductor, capacitor, and resistor, as well as the frequency of the input signal. At resonance, the impedance reaches its minimum value, allowing for maximum energy transfer between the inductor and capacitor.
Understanding impedance is crucial for designing circuits that can effectively filter and process specific frequencies, ensuring optimal performance and efficiency in various applications.
Bandwidth
Bandwidth refers to the range of frequencies that a circuit can effectively filter or process. In an LCR parallel resonance circuit, the bandwidth is determined by the circuit's quality factor (Q factor), which is a measure of how selective the circuit is in filtering frequencies. A higher Q factor indicates a narrower bandwidth and greater selectivity, while a lower Q factor results in a broader bandwidth and less selectivity.
By understanding the relationship between impedance and bandwidth, engineers can design LCR parallel resonance circuits that meet the specific requirements of their applications, ensuring optimal performance and efficiency.
How Can You Optimize an LCR Parallel Resonance Circuit?
Optimizing an LCR parallel resonance circuit involves carefully selecting and configuring the values of the inductor, capacitor, and resistor to achieve the desired performance and efficiency. Some key considerations for optimizing the circuit include:
- Component Selection: Choose high-quality components with precise values to ensure consistent performance and minimize variability due to manufacturing tolerances or environmental factors.
- Resonant Frequency: Calculate the resonant frequency using the formula \( f_r = \frac{1}{2\pi\sqrt{LC}} \) and adjust the values of the inductor and capacitor to achieve the desired frequency response.
- Quality Factor (Q Factor): Determine the Q factor of the circuit to achieve the desired bandwidth and selectivity. A higher Q factor results in a narrower bandwidth and greater selectivity, while a lower Q factor provides a broader bandwidth and less selectivity.
- Temperature Stability: Consider the effects of temperature on the performance of the circuit and select components that offer stable performance across a range of temperatures.
By addressing these considerations, engineers can design and optimize LCR parallel resonance circuits that meet the specific requirements of their applications, ensuring optimal performance and efficiency in various fields.
Troubleshooting Common Issues
When working with LCR parallel resonance circuits, engineers may encounter various issues that can affect the circuit's performance and efficiency. Some common issues and their solutions include:
- Incorrect Resonant Frequency: If the resonant frequency is not as expected, check the values of the inductor and capacitor and recalculate the resonant frequency using the formula \( f_r = \frac{1}{2\pi\sqrt{LC}} \). Ensure that the components are connected correctly and free of defects.
- High Impedance at Resonance: If the impedance is higher than expected at resonance, check for issues such as component variability, poor connections, or damaged components. Ensure that the circuit is designed and configured correctly to achieve the desired impedance.
- Unstable Performance: If the circuit exhibits unstable performance, consider the effects of temperature, component variability, and environmental factors. Select high-quality components and design the circuit to minimize the impact of these factors on performance.
- Poor Signal Quality: If the signal quality is poor, check the circuit's bandwidth and Q factor to ensure that it is optimized for the desired frequency response. Adjust the values of the inductor, capacitor, and resistor as needed to achieve the desired performance.
By identifying and addressing these common issues, engineers can troubleshoot and optimize LCR parallel resonance circuits, ensuring their effective application in various fields.
Future Developments in LCR Parallel Resonance Circuits
The field of electronics and telecommunications is constantly evolving, and the development of new technologies and materials continues to impact the design and optimization of LCR parallel resonance circuits. Some potential areas for future developments include:
- Advanced Materials: The development of advanced materials, such as high-temperature superconductors and nanomaterials, could lead to improved performance and efficiency in LCR parallel resonance circuits.
- Miniaturization: As technology continues to advance, the demand for smaller and more compact electronic components is increasing. Miniaturization of LCR parallel resonance circuits could lead to more efficient and versatile applications in various fields.
- Integration with Emerging Technologies: The integration of LCR parallel resonance circuits with emerging technologies, such as wireless communication and the Internet of Things (IoT), could lead to new applications and innovations in electronics and telecommunications.
By staying informed about these potential developments, engineers and designers can continue to optimize and innovate LCR parallel resonance circuits, ensuring their effective application in the ever-evolving field of electronics.
Frequently Asked Questions
What is the purpose of an LCR parallel resonance circuit?
The purpose of an LCR parallel resonance circuit is to filter and process specific frequencies by achieving resonance at a particular frequency. This allows for efficient signal processing and communication in various applications, such as radio transmitters and receivers, signal processing, and power systems.
How do you calculate the resonant frequency of an LCR parallel resonance circuit?
The resonant frequency of an LCR parallel resonance circuit can be calculated using the formula: \( f_r = \frac{1}{2\pi\sqrt{LC}} \), where \( f_r \) is the resonant frequency, \( L \) is the inductance, and \( C \) is the capacitance.
What are the benefits of using an LCR parallel resonance circuit?
The benefits of using an LCR parallel resonance circuit include efficient energy transfer, selective frequency filtering, versatility, cost-effectiveness, and customization. These advantages make the circuit an essential tool for engineers and designers working in electronics.
What are the limitations of an LCR parallel resonance circuit?
Some limitations of an LCR parallel resonance circuit include component variability, limited bandwidth, sensitivity to temperature, and complexity of design. Understanding and addressing these limitations is crucial for optimizing the circuit's performance and efficiency.
How does an LCR parallel resonance circuit work in radio frequency applications?
In radio frequency applications, an LCR parallel resonance circuit is used to isolate and amplify specific frequencies, enabling efficient communication over long distances. The circuit's ability to filter and process RF signals makes it an essential component in radio transmitters and receivers.
What factors should be considered when optimizing an LCR parallel resonance circuit?
When optimizing an LCR parallel resonance circuit, engineers should consider component selection, resonant frequency, quality factor (Q factor), and temperature stability. These factors are crucial for ensuring the circuit's optimal performance and efficiency in various applications.
Conclusion
The LCR parallel resonance circuit is a fundamental component in the field of electronics, offering a versatile and effective solution for filtering and processing specific frequencies. By understanding the principles of resonance, impedance, and bandwidth, engineers can design and optimize circuits that meet the specific requirements of their applications, ensuring optimal performance and efficiency.
From radio transmitters and receivers to signal processing and power systems, the LCR parallel resonance circuit plays a crucial role in various fields, providing engineers with the tools necessary to achieve efficient and reliable communication and signal processing. By staying informed about the latest developments and innovations in this field, engineers can continue to optimize and innovate LCR parallel resonance circuits, ensuring their effective application in the ever-evolving world of electronics.
For more detailed information and advanced resources, consider exploring external sources such as IEEE Xplore or Electronics Tutorials for a deeper understanding of LCR parallel resonance circuits and their applications.
You Might Also Like
The Hobbit Cast Dwarves: An In-Depth Look At The Characters And ActorsLenora Crichlow Actress: A Rising Star In British Television And Film
Optimizing Your Travel Experience: Spirit Airline LaGuardia Terminal Guide
Masked Singer Sea Queen: The Mystique And Revelations
Meet Nancy Simon: A Multifaceted Talent Shaping The Arts
Article Recommendations